Lab 3 – Odometry-based Localization

Objective

The goal of this lab is to implement a simple algorithm for odometry-based robot localization and evaluate its accuracy.

Pre-requisites

• You must have Webots R2022a (or newer) properly configured to work with Python (see Lab 1).
• You must know how to create a robot controller in Python and how to run a simulation (see Lab 1).
• You should have a working solution of Lab 2.

Robot Pose

To see the pose of the robot as calculated by Webots, click on “DEF E_PUCK E-puck” on the left menu and select “translation”. You will see the values of position and orientation of the robot (see Figure 1). You should print the position calculated by your functions at the end of each cycle, as shown in Figure 1, to facilitate comparison with the pose as calculated by Webots.

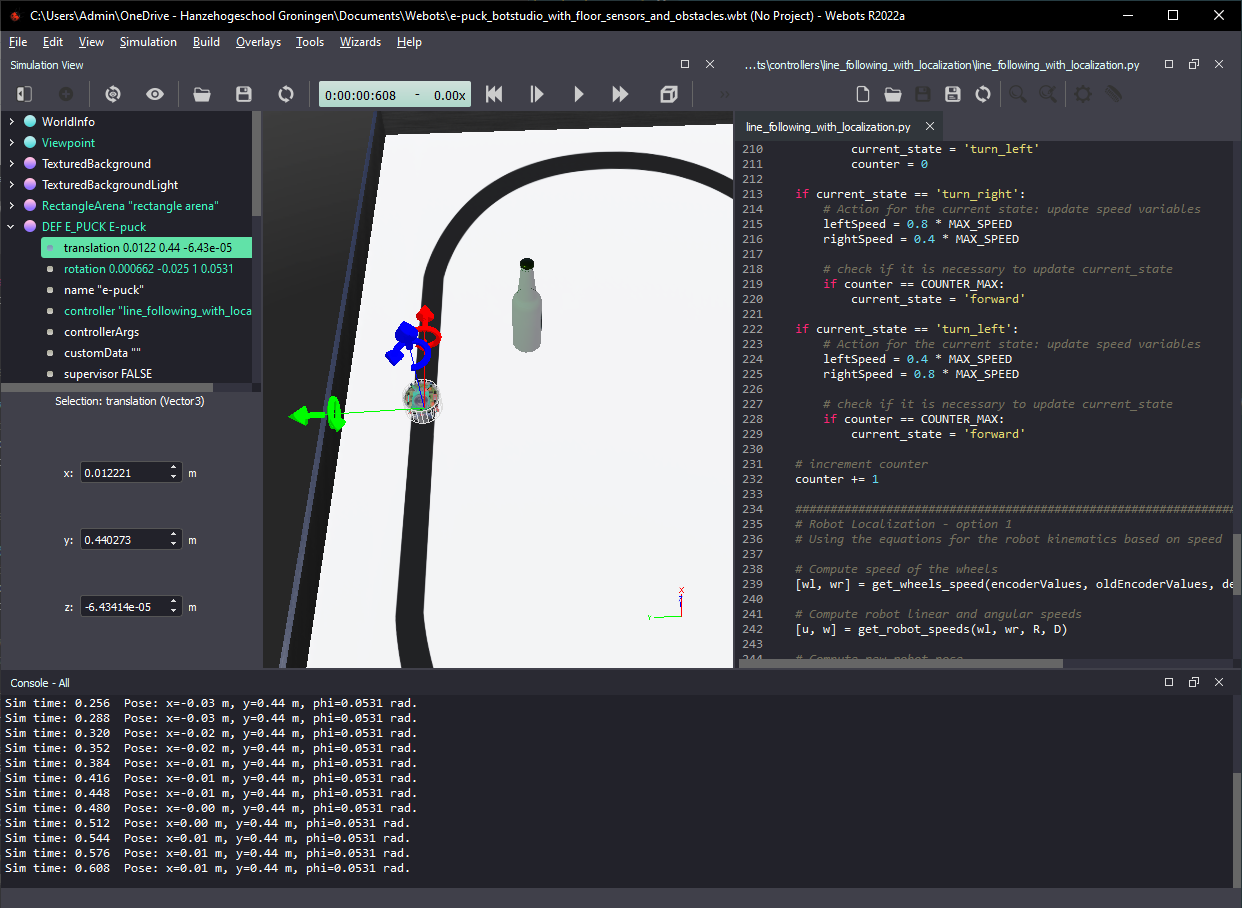
Figure 1. Webots screenshot showing robot pose calculated by the simulator (left) and by the Python code (bottom).

Tasks

Your main task is to write code to implement the functions below to add localization capability to your line-following behavior. The functions below should be called in sequence in the main loop of your program:

    # Compute speed of the wheels
    [wl, wr] = get_wheels_speed(encoderValues, oldEncoderValues, delta_t)
    
    # Compute robot linear and angular speeds
    [u, w] = get_robot_speeds(wl, wr, R, D)
    
    # Compute new robot pose
    [x, y, phi] = get_robot_pose(u, w, x, y, phi, delta_t)

The tasks are listed below:

1. Write the function get_wheels_speed(encoderValues, oldEncoderValues, delta_t) to calculate the speed of the robot wheels based on encoder readings. Test your code before moving to the next step.
2. Write the function get_robot_speeds(wl, wr, R, D) to calculate the linear and angular speeds of the robot based on the speed of its wheels. Test your code before moving to the next step.
3. Write the function get_robot_pose(u, w, x, y, phi, delta_t) to calculate the position and orientation of the robot based on its orientation and linear and angular speeds.
4. Compare the pose calculated by your functions with the pose calculated by Webots in different moments of the simulation.

Some information for implementing the code

The definition of the variables used in the functions is given below.

Robot pose and speed in (x,y) coordinates:
x = position in x [m]
y = position in y [m]
phi = orientation [rad]
dx = speed in x [m/s]
dy = speed in y [m/s]
dphi = orientation speed [rad/s]

Robot wheel speeds:
wl = angular speed of the left wheel [rad/s]
wr = angular speed of the right wheel [rad/s]

Robot linear and angular speeds:
u = linear speed [m/s]
w = angular speed [rad/s]

Period of the cycle:
delta_t = time step [s]

To calculate robot localization you will need to use some physical parameters of the robot:

R = radius of the wheels [m]: 20.5mm 
D = distance between the wheels [m]: 52mm 

You can use the pieces of code below to initialize the encoder sensors and to read encoder values in the main loop of your program:

To initialize encoders:

encoder = []
encoderNames = ['left wheel sensor', 'right wheel sensor']
for i in range(2):
    encoder.append(robot.getDevice(encoderNames[i]))
    encoder[i].enable(timestep)

To read the encoders in the main loop:

    encoderValues = []
    for i in range(2):
        encoderValues.append(encoder[i].getValue())    # [rad]

The encoder values are incremented when the corresponding wheel moves forwards and decremented when it moves backwards.

Think about the following questions

• How accurate is the odometry-based localization?
• In what conditions is odometry-based localication useful? And when is it problematic?

Solution

A partial solution is provided for this lab. I recommend you first try to modify your line following code from Lab 2 to implement the localization as described above. If you need inspiration, you can use the provided template.

If you need extra explanation, check the Jupyter Notebook for Odometry-based Localization.

Challenge: 1-D Kalman Filter

Use another sensor (like a compass or gyroscope) to estimate the orientation of the robot. Implement a 1-D Kalman Filter to combine the values given by this extra sensor with the orientation calculated via odometry to get a better estimate of the robot orientation.

No solution is provided for the challenge. In this post you find explanation about the 1-D Kalman Filter and how to implement it in Python.

Conclusion

After following this lab you should know more about the implementation and limitations of odometry-based localization for mobile robots.

Next Lab

Go to Lab 4 - Go-to-goal behavior with PID

Back to main page.