Lab 4 – Go-to-goal behavior with PID

Objective

The goal of this lab is to implement a go-to-goal behavior based on a PID controller. Figure 1 illustrates the go-to-goal implementation for 2 positions in a sequence.

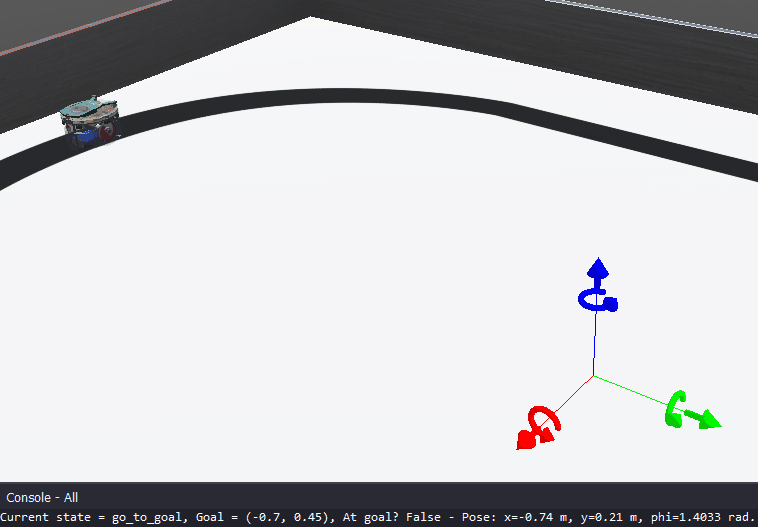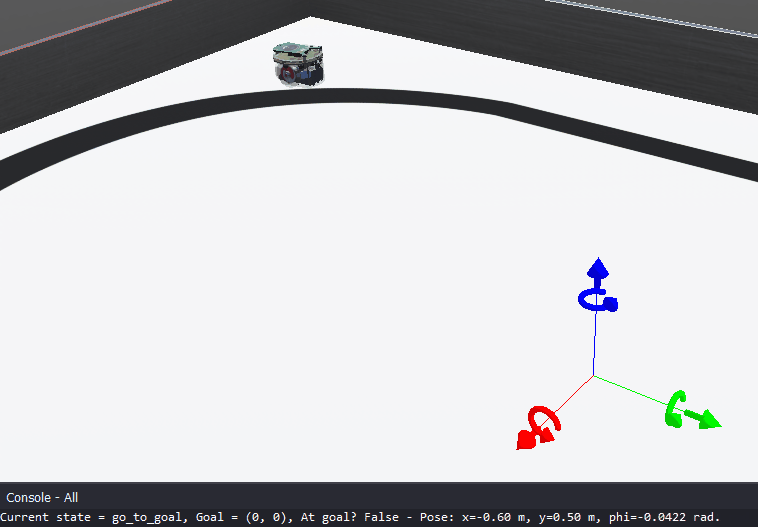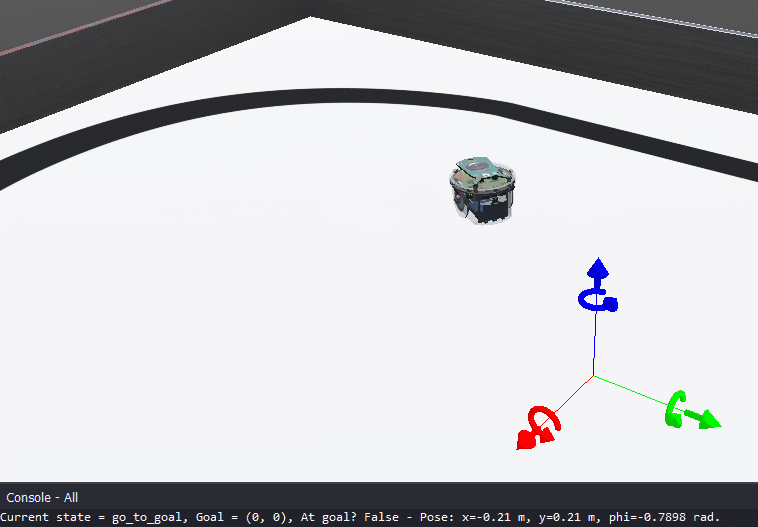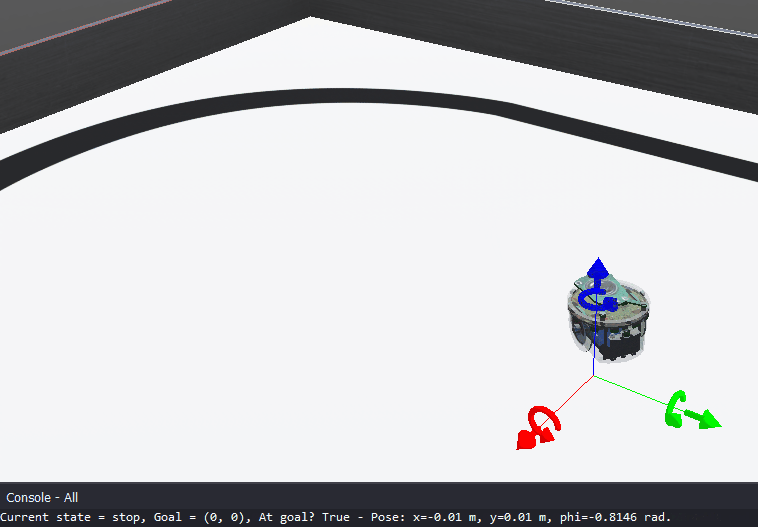
Go to goal illustration

Figure 1. Illustration of the Go-to-Goal controller reaching two goals in sequence. After reaching the final goal, the robot stops.

Pre-requisites

You must have Webots R2022a (or newer) properly configured to work with Python (see Lab 1).
You must know how to create a robot controller in Python and how to run a simulation (see Lab 1).
You should have a working solution of Lab 3.

Tasks

Your main task is to write code to implement the PID controller to control the robot orientation. Note that the PID controller needs information about the actual robot orientation, so the odometry-based localization algorithm implemented in Lab 3 needs to be working. You are going to modify the line-following behavior to add the go-to-goal behavior, which will be activated by a new state in your state machine.

The tasks are detailed below:

1- Create a function to calculate position and orientation errors based on the estimated and desired positions of the robot. An example is shown below:

import numpy as np

# Position error:
x_err = xd - x
y_err = yd – y
dist_err = np.sqrt(x_err**2 + y_err**2)

# Orientation error
phi_d = np.arctan2(y_err,x_err)
phi_err = phi_d – phi

# Limit the error to (-pi, pi):
phi_err_correct = np.arctan2(np.sin(phi_err),np.cos(phi_err))

2- Create a new function that implements a “go-to-goal” behavior using a PID controller. Your PID controller must control the robot orientation by adjusting its angular speed. A simple implementation of a PID controller is illustrated below:

# PID algortithm: must be executed every delta_t seconds
# The error is calculated as: e = desired_value - actual_value

P = kp * e                      # Proportional term; kp is the proportional gain
I = e_acc + ki * e * delta_t    # Intergral term; ki is the integral gain
D = kd * (e - e_prev)/delta_t   # Derivative term; kd is the derivative gain

output = P + I + D              # controller output

# store values for the next iteration
e_prev = e     # error value in the previous interation (to calculate the derivative term)
e_acc = I      # accumulated error value (to calculate the integral term)

3- Using the code from Lab 3, create a new “go-to-goal” state that is activated when the robot reaches approximately half of the track. In other words, the robot starts by following the line using the state-machine with localization implemented in lab 3. When it gets half-way through the path, the new “go-to-goal” state is activated.

A list of goal positions is given in the program. One should be able to add as many goal positions as desired. After reaching the final goal position, the robot must stop.

Implement your code so that the robot goes from its current position to the next goal position, stops, and stays there for some short time (1 second, for example). Then, the robot should move to the subsequent goal position and repeat the cycle until it reaches the final goal position. Everytime the robot stops at a goal, it has to print its own position and distance error to the goal.

4- Test your code by making the robot go to the 4 corners of the field (without touching the walls), and then to the center of the field.

Actuator Saturation

The desired speeds for the left and right wheels will be calculated from the desired values of linear and/or angular speeds. If the desired speed for one of the wheels is higher than the maximum speed that its motor can achieve, the wheel will not be able to follow the speed desired by the controller. We say that there is actuator saturation. In this case, the difference between the speeds of the left and right wheels will be smaller than expected, which will cause the robot to turn at a different angular speed than desired by the PID controller. As a result, the robot will not turn to the direction of the goal. And if both motors are saturated, the robot will not turn at all!

Actuator saturation is a potential problem in all control systems, so we need to keep it in mind. In the case of the “go-to-goal” controller for the differential-drive robot, it is very important that the robot drives towards the correct direction, and no so important that it moves with the desired linear speed. Therefore, we can avoid the saturation problem by reducing the overall robot speed while maintaining its angular speed.

The code below implements the solution discussed above by calculating a speed_ratio. When saturation occurs, one of the motors will have its speed reduced so that the desired speed ratio is maintained.

def wheel_speed_commands(u_d, w_d, d, r):
    """Convert desired robot speeds to desired wheel speeds"""
    wr_d = float((2 * u_d + d * w_d) / (2 * r))
    wl_d = float((2 * u_d - d * w_d) / (2 * r))
    
    # If saturated, correct speeds to keep the original turning ratio
    if np.abs(wl_d) > MAX_SPEED or np.abs(wr_d) > MAX_SPEED:
        speed_ratio = np.abs(wr_d)/np.abs(wl_d)
        if speed_ratio > 1:
            wr_d = np.sign(wr_d)*MAX_SPEED
            wl_d = np.sign(wl_d)*MAX_SPEED/speed_ratio
        else:
            wl_d = np.sign(wl_d)*MAX_SPEED
            wr_d = np.sign(wr_d)*MAX_SPEED*speed_ratio
    
    return wl_d, wr_d

Compare the controller performance with and without the saturation correction.

Think about the following question

What do you need to change in your code to control the orientation of the robot at the goal?

Try to modify your line following code with localization from Lab 3 to implement the go-to-goal behavior as described above.

Solution

No solution is provided for this lab. If you need extra explanation, check the Jupyter Notebook for Mobile Robot Control with PID.

Conclusion

After following this lab you should know how to implement a moving controller using a PID to take a mobile robot to specific positions defined by their coordinates.

Next Lab

Go to Lab 5 - Combine Behaviors to Complete a Mission

Back to main page.